- VEHICLE
INTELLIGENCE & TRANSPORTATION ANALYSIS LABORATORY
University of California, Santa Barbara
![]()

University of California, Santa Barbara
|
 |

|
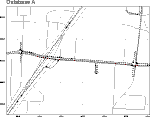
The red base map lines in this illustration are from vendor Knopf Engineering (Visalia CA), which claims an accuracy of about 0.6 metres, 55% of the time. Driving eastbound and westbound down a major artery (horizontal line), the vehicle track straddles the centerline, as it should. When the vehicle takes U-turns on side streets, the correspondence between the vehicle path and database is striking. On the freeway (oblique parallel lines left of center) the vehicle path runs almost exactly down the centerline of the northbound and southbound carriageways. If all street network data were this accurate, interoperability problems would be minimal. |
|
Using another
reference database with the same drive path as above, significant positional
errors are evident in the database. Note the gross generalization
of the ramp off the northbound carriageway of the freeway. The grid
interval is 200m.
This database is more typical of the commercial offerings currently on the market. In fairness to these map database vendors, they serve a different market, and their price is more than an order of magnitude below that of the engineering-grade product above. |
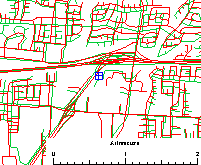
A graphic overlay is a simple
yet dramatic way to illustrate the extent of disagreement, and the kinds
of locations where disagreement is most likely to occur. In the illustrations
below, data bases for a section of Goleta (suburban Santa Barbara) are
overlaid in pairs, one in red, the other in green. Discordances of
up to 100 metres are routinely observed
in some neighbourhoods, while in other areas there is better agreement.
In the case of Map 5 (B vs F), one is known to be derived from the other;
this is evident from the close agreement.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
It is fair to
argue that when two maps disagree, one or both contain error. Examining
a small section of one of the above maps closely, we find two types of
error:
|
 |
| Positional disagreement
can be studied by identifying a set of points in one data base, finding
the corresponding points in the other data base, and measuring the vector
or positional difference between the two points. The easiest points
of correspondence to study are intersections. They can be automatically
identified with reference to the names of the intersecting streets (the
process is not error-proof see our comments on the Cross-Streets
Profile).
In the figures below, intersections
have been identified automatically within a small neighborhood in Goleta,
California. The databases are in red and green, the vectors in black.
|
| The set of black
vectors may be considered a sample of a vector field, i.e. at every point
on the map there is a local error, of which the yellow vectors represent
a sample. At VITAL we are trying to characterize error fields
in different ways. If the magnitude and direction of error is consistent
in one portion of the map, it would suggest that that area was surveyed
or digitized at the same time, by the same operator, with a constant error.
Once we have a satisfactory means of modelling error, we can consider the
error at any point to be a function of two components: (a) systematic error
as characterized by the field, and (b) random error at the point.
Error due to (a) can be corrected, leaving only random residual error.
Two of our technical reports (Church et al, 1998; Funk et al, 1998) describe our most recent efforts in error modeling. |

|